Decimal to Binary

This Decimal to Binary Converter is a handy tool that can effortlessly convert decimal numbers into binary format. Input your decimal number, specify the number of decimal places (if applicable), and click "Convert" to instantly get the binary equivalent.

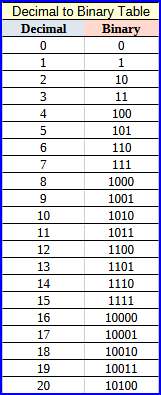
Decimal to binary conversion involves transforming a decimal (base-10) number into its binary (base-2) representation. In the binary system, each digit is either 0 or 1, and the positions of the digits represent powers of 2.

Decimal to Binary Converter

Decimal:
base₁₀

Decimal Places:
#

Result:

Binary Output:
base₂

Convert decimal numbers to binary quickly and easily with our online tool.

Calculator

enter any decimal number you wish to convert into binary
specify the number of decimal places for precision

Result

the binary equivalent of the entered decimal number

Here's how the conversion works:

Integer Part Conversion:

Divide the decimal number by 2
Record the remainder (0 or 1), representing the least significant bit (LSB)
Repeat the division process with the quotient until it becomes zero
The binary equivalent is obtained by reading the remainders in reverse order

Fractional Part Conversion (if applicable):

Multiply the fractional part by 2
Record the integer part of the result, which represents the next bit after the decimal point
Repeat the multiplication process with the fractional part until it becomes zero or until the desired precision is reached.

Example Conversion:

Convert the decimal number 13.625 to binary.

Integer Part Conversion:

Dividing 13 by 2, we get quotient 6 and remainder 1
Dividing 6 by 2, we get quotient 3 and remainder 0
Dividing 3 by 2, we get quotient 1 and remainder 1
Dividing 1 by 2, we get quotient 0 and remainder 1
Reading the remainders in reverse order: 1101

Fractional Part Conversion:

Multiplying 0.625 by 2, we get 1.25, so the first bit after the decimal point is 1
Multiplying 0.25 by 2, we get 0.5, so the next bit is 0
Multiplying 0.5 by 2, we get 1, so the next bit is 1
Multiplying 0 by 2, we get 0. (Terminating because no more precision is required)

Binary Equivalent:

Combining the integer and fractional parts, we get:

Integer part: 1101
Fractional part: .101
Binary equivalent: 1101.101

The decimal number 13.625 is equivalent to 1101.101 in binary notation.

Decimal to Binary